On observe des spirales dans divers végétaux. Pourquoi la nature semble-t-elle tant apprécier ces formes?
Si l’on regarde un ananas, les écailles semblent former des spirales. Si on prend le temps de les compter, on en observe 8 dans un sens et 13 dans l’autre. Promenons-nous dans les bois et prenons le temps de ramasser des cônes de conifères. Regardons-les du dessous. Ils présentent tous des spirales dans les deux directions. Le nombre de spirales dépend de l’espèce de conifère. Pour le pin blanc, on observe 3 spirales dans un sens et 5 dans l’autre. Les cônes d’autres variétés de conifères peuvent avoir 5 spirales dans un sens et 8 dans l’autre, ou encore 8 dans un sens et 13 dans l’autre. Vous remarquerez que les spirales sont plus faciles à compter dans un sens que dans l’autre!
Nous pouvons faire la même expérience avec les fleurs de tournesol. Il existe des fleurs avec 13 spirales dans un sens et 21 dans l’autre, ou encore avec 21 spirales dans un sens et 34 dans l’autre, ou même avec 34 spirales dans un sens et 55 dans l’autre. L’observation de cette particularité remonte au XIXe siècle.
Suite de Fibonacci
La suite de Fibonacci est la suite célèbre:
\[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …\]
solution d’un problème sur la croissance de lapins posé par Léonard de Pise dans le Liber Abaci, publié en 1202. Dans cette suite, tout nombre est la somme des deux précédents:
\[2=1+1, 3=1+2, 5=2+3, 8=3+5, \: \text{etc.}\]
Prenons deux nombres consécutifs de la suite de Fibonacci, \(a_n\) et \(a_{n+1},\) et considérons la suite des quotients:
\[b_n=\frac{a_{n+1}}{a_n}\]
dont les premiers termes sont:
\[1,2,\frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \frac{13}{8},\ldots\]
On peut montrer que la suite \(b_n\) converge vers le nombre d’or1:
\[\phi=\frac{1+\sqrt{5}}{2}.\]
Nous admettrons ce résultat dont la preuve demande un peu de travail.
Dans tous les cas, les nombres de spirales dans un sens et dans l’autre sont deux nombres consécutifs de la suite de Fibonacci! Mais pourquoi?
Ce n’est que récemment que Douady et Couder ont donné une explication au processus de formation des spirales par le biais d’une modélisation mathématique produisant les résultats décrits plus haut.
Nous allons décrire l’idée de base qui sous-tend cette explication concernant la fleur de tournesol. Les graines de cette fleur sont appelées primordia. Lors de la croissance de la fleur, elles se forment au centre et s’en éloignent ensuite vers l’extérieur. Quel est l’angle entre deux primordia consécutifs? La nature s’arrange pour que les primordia remplissent tout l’espace disponible. Si l’angle entre deux primordia était de la forme:
\[\frac{p}{q}2\pi,\]
soit un multiple rationnel de \(2\pi\), alors les primordia s’aligneraient sur q rayons faisant un angle de \(2\pi/q\) entre eux. Dès qu’on s’éloignerait du centre, il resterait du vide. Donc, il vaut mieux choisir un multiple irrationnel de \(2\pi\) comme angle entre deux primordia consécutifs. Mais lequel? Nous allons discuter du fait que tous les irrationnels ne sont pas égaux et que certains sont plus « irrationnels » que d’autres!
Nous avons l’habitude de représenter les nombres réels comme les points d’une droite et nous connaissons la propriété suivante:
Entre deux nombres rationnels, il y a un nombre irrationnel et entre deux nombres irrationnels, il y a un nombre rationnel.
Avant même de savoir démontrer que \(\pi\) est un nombre irrationnel, les anciens cherchaient à l’approximer par des nombres rationnels \(p/q\):
\[3, \frac{22}{7}, \frac{333}{106}, \frac{335}{113}, \: \text{etc.}\]
Lorsqu’un nombre \(\alpha\) est irrationnel, il n’est égal à aucune fraction \(p /q\). Chaque fois qu’on trouve une fraction \(p/q\) qui l’approxime, on peut se demander quel est le reste:
\[r=\alpha-\frac{p}{q}.\]
Ce reste \(r\) peut être aussi petit que l’on veut. Pour obtenir un reste plus petit il faut choisir une fraction \(p/q\) avec \(p\) et \(q\) plus grands.
Donc, ce qui nous intéresse, c’est la taille du reste r en fonction de la taille de p et q.
On dira qu’un nombre irrationnel \(\alpha\) est mal approximé par les rationnels si toute suite \(p_n/q_n\) d’approximations rationnelles de \(\alpha\) est telle que la suite des restes:
\[r_n=\alpha-\frac{p_n}{q_n} \: \text{satisfait} \: |r_n|>\frac{C}{q_{n}^{\beta}},\]
où \(C\) et \(\beta\) sont des constantes positives.
Un tel nombre irrationnel est appelé diophantien. Dans le cas contraire, si \(\alpha\) est bien approximé par les rationnels, il est dit liouvillien. Mais, comment peut-on décider si un nombre irrationnel est diophantien ou liouvillien? Il existe un outil très puissant: la fraction continue du nombre irrationnel.
Nombre réel et fraction continue
Tout nombre réel positif \(\alpha\) a une écriture en fraction continue. Comment la trouve t-on? Soit \(a_0\) la partie entière de \(\alpha\), alors on peut écrire \(\alpha=a_0 +\alpha_0\),où \(\alpha_0 \in [0,1[.\) Si \(\alpha_0 =0\), la fraction continue se termine là. Sinon, on pose \(\alpha_0 = 1/ \beta_0\). Alors, \(\beta_0 > 1\). Soit \(a_1\) la partie entière de \(\beta_0\). Alors, \(\beta_0 = a_1 + \alpha_1\), où \(\alpha_1 \in [0,1[\). Si \(\alpha_1 = 0,\) la fraction continue se termine là. Sinon, on pose \(\alpha_1 = 1/\beta_1\). Alors, \(\beta_1 > 1\). On itère…. Ceci donne l’écriture:
\[\alpha=a_0+ \cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{a_3+\cdots}}}\]
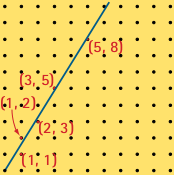où les \(a_n\) sont des entiers positifs. L’écriture est finie si le nombre est rationnel et infinie pour un nombre irrationnel. Dans le cas d’un nombre a irrationnel, si on s’arrête après un nombre fini d’itérations et qu’on néglige le reste \(\alpha_n\), on obtient une suite d’approximations rationnelles \(p_n/q_n\) du nombre \(\alpha\). Ces approximations rationnelles sont appelées les réduites de la fraction continue. La suite \(\{p_n/q_n\}\) a une propriété remarquable. Parmi tous les nombres rationnels de la forme \(p/q\), avec \(q ≤ qn, p_n/q_n\) est la meilleure approximation de \(\alpha\). Nous allons visualiser cette propriété comme ceci. Prenons une planche sur laquelle nous plantons des clous à tous les points à coordonnées entières (voir figure). Traçons la droite \(y = \alpha x\) de pente \(\alpha\). Bien sûr, elle ne passe par aucun de ces points, sauf l’origine. Les bonnes approximations rationnelles \(p/q\) de \(\alpha\) correspondent aux points \((p,q)\) qui sont proches de la droite. Accrochons un fil à l’infini le long de la droite et levons ou baissons le fil. Quels sont les points qu’il accroche? Ce sont précisément les points \((p_n, q_n)\) correspondant aux réduites \(p_n/q_n\) de la fraction continue tronquée!
Fraction continue
Avant de définir la fraction continue du nombre irrationnel dans le cas général, regardons le nombre d’or.
\[\phi=\frac{1+\sqrt{5}}{2}.\]
Il est racine de l’équation caractéristique \(\phi^2 – \phi – 1 = 0\), ce qui nous donne \(\phi^2=\phi+1\). Si nous divisons par \(\phi\), on obtient:
\[\phi =1+\frac{1}{\phi}. \: (^*)\]
Remplaçons l’occurrence de \(\phi\) au dénominateur par la valeur donnée par \((^*)\):
\[ \phi=1+ \cfrac{1}{1+\displaystyle \frac{1}{\phi}}\]
En itérant, on obtient:
\[\phi=1+ \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\displaystyle \frac{1}{\phi}}}}\]
On voit bien qu’on est conduit à la limite à écrire une fraction infinie:
\[\phi=1+ \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}}}.\]
C’est l’écriture de \(\phi\) comme fraction continue. Si, au lieu de regarder la fraction continue, on s’arrête après un nombre fini d‘itérations et qu’on néglige le terme \(1/\phi\), on obtient les approximations successives:
\[1, 2, \frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \frac{13}{8}, \ldots\]
qui sont précisément les quotients de deux nombres consécutifs de Fibonacci!
Nous avons dit qu’un nombre irrationnel a une écriture comme fraction continue infinie. La réciproque est aussi vraie: si on a une fraction continue infinie:
\[\alpha=a_0+ \cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{a_3+\cdots}}}\]
alors elle représente un nombre irrationnel. Toute suite \(\{a_n\}\) d’entiers positifs est permise. Prenons maintenant une réduite \(p_n/q_n\) correspondant à tronquer la fraction continue après \(a_n\). Il est facile de se convaincre que, plus \(a_{n+1}\) est grand, plus la différence entre \(\alpha\) et la réduite \(p_n/q_n\) est petite, et mieux \(\alpha\) est approximé par les rationnels. Au contraire, plus \(a_{n+1}\) est petit, et moins bonne est l’approximation. Quand l’approximation est-elle la moins bonne? Quand tous les \(a_n\) sont égaux à 1!
Nous venons de montrer que le nombre d’or est le nombre irrationnel le moins bien approximé par des nombres rationnels.
Coeur de tournesol
Revenons à la formation des spirales dans la fleur de tournesol. Le premier primordium apparaît d’un côté de l’apex, par exemple à droite, et s’en éloigne. Le second apparaît du côté opposé, soit à gauche. Le troisième apparaît en haut ou en bas. C’est ce qui déterminera le sens des spirales. Après un certain nombre de primordia, l’angle entre deux primordia consécutifs tend vers le nombre d’or.
Stéphane Douady et Yves Couder ont proposé la modélisation suivante du phénomène en se basant sur les règles de Hofmeister qui caractérisent la croissance botanique:
- les primordia naissent sur le bord de l’apex et s’en éloignent radialement;
- les primordia apparaissent périodiquement;
- un nouveau primordium nait dans le plus grand espace disponible laissé par les précédents.
Pour modéliser la propriété 3, Douady et Couder ont utilisé des gouttes d’un ferrofluide qui se repoussent mutuellement. L’expérience qu’ils ont faite est la suivante. On remplit un récipient cylindrique d’huile. On fait tomber au centre du récipient des gouttelettes de ferrofluide. Un champ magnétique minimum au centre et maximum à l’extérieur attire les gouttelettes vers la paroi externe du récipient.
Au centre du plat, se trouve une petite protubérance simulant l’apex et forçant les gouttes à glisser sur ce qui simule le bord de l’apex. Comme les gouttelettes se repoussent entre elles, la nouvelle gouttelette glisse sur le bord de la protubérance du côté où l’espace disponible est le plus grand. Ceci détermine la direction radiale dans laquelle elle va migrer vers la paroi externe du récipient. Ces gouttelettes se comportent donc exactement comme les primordia qu’on a décrits ci-dessus.
On observe alors deux ensembles de spirales, l’une dans un sens et l’autre dans le sens inverse. Les nombres respectifs de ces spirales sont toujours deux nombres consécutifs de la suite de Fibonacci. Lesquels? Cela dépend de la vitesse à laquelle les gouttelettes migrent vers le bord du récipient, du rayon de l’apex, et également de l’intervalle de temps entre deux gouttelettes consécutives (voir encadré: simulation).
La simulation
Nos simulations numériques effectuées dans le cadre fixé par les règles de Hofmeister confirment les résultats de l’expérience de Douady et Couder et les simulations réalisées par ces deux auteurs. Les primordia apparaissent à intervalles réguliers T sur un cercle C de rayon \(R_0\). Après leur apparition, on leur impose un mouvement radial avec une vitesse \(V (r) \propto r\), où \(r\) est la distance d’un primordium au centre du cercle. En intégrant les équations de mouvement avec les conditions initiales \(V(t = 0) = V_0, r (t = 0) = R_0,\) la distance radiale du primordium et sa vitesse seront données par:
\[r(t) = R_0 \exp(V_0 t/R_0)\]
et
\[V(t)=V_0 \exp(V_0 t/R_0).\]
Le rapport des distances au centre de deux primordia successifs, appelé rapport plastochronique, est égal à \(\exp(G)\) où \(G = V_0 T/R_0\). Le système considéré ne dépend que de ce seul paramètre sans dimension. Pour trouver la position angulaire de l’apparition d’un primordium sur le cercle C, on suppose que toutes les particules se repoussent avec une force dérivant d’un potentiel \(\propto 1/d^3\), où \(d\) est la distance entre un primordium et un point de C (un potentiel \(\propto 1/d\) donne les mêmes résultats). L’endroit d’apparition du nouvel élément sur C est trouvé ainsi: en chaque point du cercle on calcule l’énergie potentielle comme la somme des contributions de tous les primordia déjà apparus. La position angulaire du nouvel élément est celle pour laquelle l’énergie potentielle totale est minimale (ce minimum est obtenu numériquement). En fait on obtient une meilleure modélisation biologique si \(G\), ou d’une manière équivalente T, décroit exponentiellement en fonction du nombre de primordia pour s’approcher d’une limite lorsque n est assez grand. Pour obtenir la configuration reproduite ci-dessous avec 13 spirales s’enroulant à droite et 21 spirales s’enroulant à gauche, nous avons pris la fonction:
\[G(n) = a + b/ \exp[(n – 1)/c],\]
où \(n\) est le nombre de primordia avec \(a = 0,01, b=0,99\) et \(c=6.\)
Pour reproduire la distribution des graines au cœur d’un tournesol, on doit ajouter à \(G(n)\) l’expression:
\[ 0,5 \log[(N – n + 1)/(N – n)], \]
où N représente le nombre total de graines. On a obtenu la configuration reproduite plus bas avec \(N=500,a=0,b=1\) et \(c=17\).
Pour voir une illustration animée de nos simulations, vous pouvez télécharger les fichiers Spirales.jar et Tournesol.jar à partir de www.accromath.ca. Lors du téléchargement, enregistrez ou renommez les fichiers avec l’extension .jar uniquement. Pour faire démarrer les animations, il suffit alors de cliquer deux fois dessus. Si les animations ne démarrent pas, il faut installer le Java Runtime Environment sur votre ordinateur, que vous pouvez facile- ment télécharger à partir de:
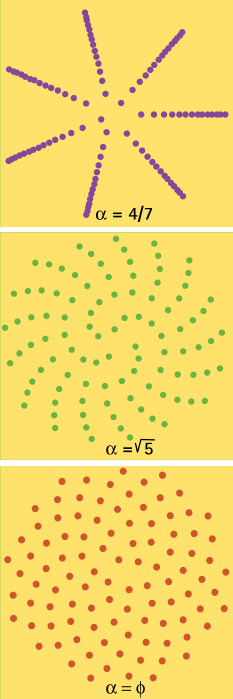Un modèle simple
Certaines configurations de graines comme dans le cœur d’un tournesol sont approximées par un réseau ou maillage spiral d’un type spécial. Un réseau spiral est une configuration de points placés sur des cercles concentriques tel que:
- il n’y a qu’un seul point par cercle;
- l’angle de divergence \(\delta = 2\pi \times \alpha\) entre deux points situés sur deux cercles successifs est constant (\(\alpha\) représente donc la fraction de tour);
- les rayons de deux cercles successifs augmentent selon une règle particulière au réseau. Dans le cas du tournesol, le rayon du \(n^e\) cercle est donné par la règle \(r(n)=\sqrt{n \times P}\), où \(P\) est une constante positive.
Les coordonnées polaires du \(n^e\) point du réseau sont donc données par:
\[\left \{ \begin{array}{r c l}r(n)&=&\sqrt{n \times P} \\ \theta(n) &= &n \times 2 \pi \times \alpha \end{array} \right . \]
Seule la partie décimale de \(\alpha\) est importante; la partie entière nous fait revenir au même point. Pour obtenir d’autres figures en faisant varier \(\alpha\), vous pouvez télécharger le fichier Maillage.xls sur www.accromath.ca.
Pour en s\(\alpha\)voirplus !
S. Douady et Y. Couder, La physique des spirales végétales, La Recherche, 250, 28 (1993). http://maven.smith.edu/~phyllo/Gallery/index.html (Pour voir le film de l’expérience de Douady et Couder.).
- Voir Nautile, nombre d’or et spirale dorée, en page 8 de ce numéro et l’encadré Léonard de Pise en page 19, vol. 3, hiver-printemps 2008. ↩
