Pavages hyperboliques (secondaire)
- Par définition, la « droite hyperbolique » intercepte la périphérie de \(U\) à angle droit.
Ainsi, le rayon de \(U\) et celui de \(C,\) marqués sur la figure, forment un angle droit. La trigonométrie lie l’angle \(a\) au rayon \(r\):
\( \tan a =r \), puisque le rayon de \(U\) est 1
et le théorème de Pythagore donne \(1 + r^2 = d^2,\) ou encore \(d^2 =1+\tan^2 a.\)
-
- Appelons \(Q\) un des deux points d’intersection obtenus en traçant le cercle de rayon \(OP.\) Les deux triangles \(OPQ\) et \(OQP’\) sont isocèles. De plus, ils partagent l’angle en \(O\) qui, dans les deux triangles, est un de ceux de la paire d’angles égaux. Les deux triangles sont donc semblables. Le rapport du petit côté sur le grand est le même pour les deux triangles, c’est-à-dire,
\[ \frac{\overline{OP’}}{r}=\frac{r}{\overline{OP}}.\]
Par conséquent, \(\overline{OP} \cdot \overline{OP’} = r^2\) qui est l’égalité annoncée. - Par définition de l’inversion, l’image \(P’\) d’un point \(P\) par l’inversion par rapport au cercle de centre \(O\) et rayon \(r\) doit être tel que \(\overline{OP} \cdot \overline{OP’}=r^2.\) Si le point \(P\) est sur le cercle d’inversion, alors \(\overline{OP} = r\) et il suffit de prendre \(P’ = P\) pour que la relation soit satisfaite.La validité de la construction utilisée en a) a été démontrée pour un point \(P\) extérieur au cercle d’inversion. Mais cette construction peut être étendue pour les points sur le cercle et certains à l’intérieur. (Pourriez-vous dire pour lesquels?) Pour un point \(P\) sur le cercle d’inversion, le triangle \(OPQ\) de la solution de a) est équilatéral et \(P\) et \(P’\) sont alors confondus.
- L’inversion transforme les cercles en cercles. Ainsi, la périphérie \(D\) de \(U\) sera transformée en un cercle. Par continuité, l’exercice sera terminé si nous montrons que la périphérie \(D\) est envoyée sur elle-même par l’inversion décrite dans l’énoncé.Soit \(C\) un cercle d’inversion intersectant la périphérie \(D\) à angles droits. Par b), les deux points où le cercle \(C\) intersecte \(D\) sont fixes sous l’inversion. Puisqu’un cercle est déterminé par trois de ses points, il suffit de trouver un troisième point de \(D\) qui est également envoyé sur \(D.\) Soit \(P,\) le point de \(D\) le plus loin de \(O.\)
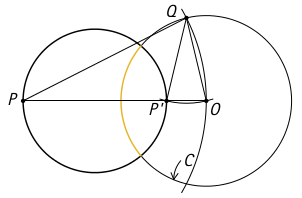En utilisant la notation du premier exercice, le segment \(OP\) est de longueur \(1+d.\) Si \(r\) est le rayon de \(C,\) l’image \(P’\) de \(P\) par l’inversion doit déterminer un segment de longueur
\[ \overline{OP’}=\frac{r^2}{d+1}. \]
Mais le premier exercice a montré que \(1+r^2 =d^2\) et donc
\[ \overline{OP’}=\frac{r^2}{d+1}=\frac{d^2-1}{d+1}=\frac{(d-1)(d+1)}{d+1}=d-1.\]
Le point \(P’\) est donc à distance \(d-1\) de \(O,\) c’est-à-dire à distance \(1\) du centre de \(U.\) Il est donc sur \(D.\)
- Appelons \(Q\) un des deux points d’intersection obtenus en traçant le cercle de rayon \(OP.\) Les deux triangles \(OPQ\) et \(OQP’\) sont isocèles. De plus, ils partagent l’angle en \(O\) qui, dans les deux triangles, est un de ceux de la paire d’angles égaux. Les deux triangles sont donc semblables. Le rapport du petit côté sur le grand est le même pour les deux triangles, c’est-à-dire,
Triangles d’or
- Pour diviser le triangle isocèle TA en deux triangles isocèles, TA et TO, il suffit de reporter le petit côté sur le grand en traçant un arc de cercle centré en un sommet opposé aux côtés congruents et dont le rayon est le petit côté.
En appliquant la même procédure au triangle de plus grande aire, on obtient :
On remarque qu’on a toujours deux possibilités pour choisir un sommet comme centre de l’arc de cercle. Cela signifie qu’il existe plusieurs solutions au problème de regrouper les triangles pour former un triangle semblable au triangle aigu.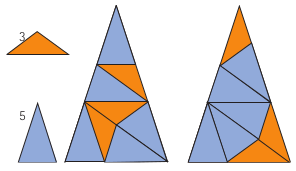
- En appliquant la même démarche qu’au numéro 1, on obtient :
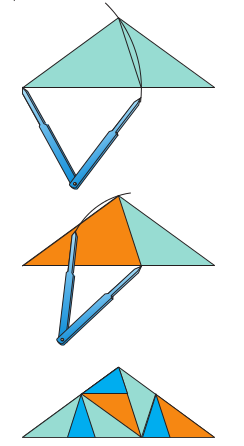
- On peut former les tangrams en imprimant les figures sur carton et en découpant suivant les lignes de subdivision.
