Combien faut-il de caméras pour surveiller chaque recoin d’une galerie d’art et où faut-il les placer ? Ce problème simple à énoncer, appelé problème de la galerie d’art, est devenu un champ de recherche de la géométrie algorithmique. Des algorithmes très astucieux permettent de borner le nombre de caméras et de déterminer où les placer. On parlera aussi du problème « dual », le problème de la forteresse, qui consiste à placer des caméras en nombre minimal pour surveiller l’extérieur d’une forteresse.
La galerie d’art
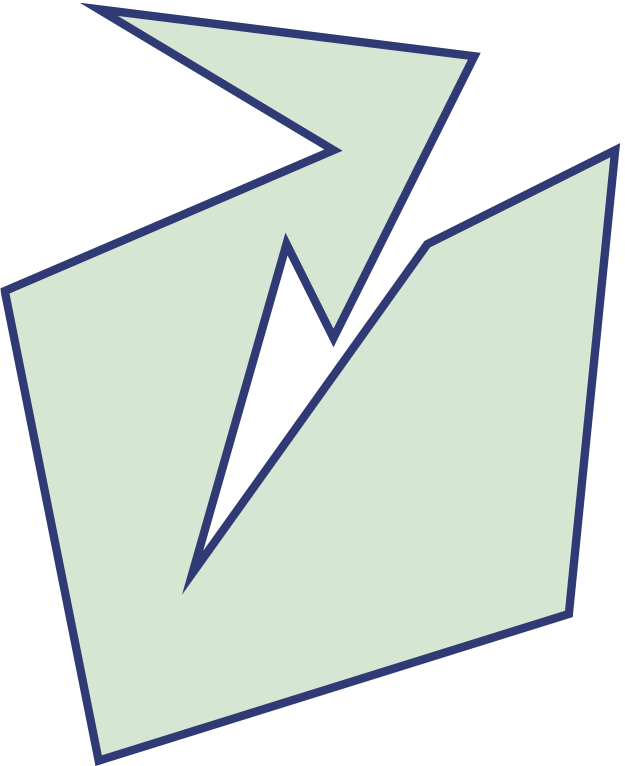Dans le problème de la galerie d’art, la galerie est l’intérieur d’un polygone à \(n\) côtés et on doit placer un minimum de caméras à des sommets du polygone pour pouvoir surveiller toute la superficie de la galerie. En voici une à gauche pour laquelle deux caméras sont nécessaires.
Pour qu’une caméra surveille un point il faut que le segment joignant le point à la caméra soit entièrement contenu dans le polygone. La seconde figure présente la région surveillée par une première caméra. La troisième est la région surveillée par une deuxième caméra. Les deux caméras, quatrième figure, surveillent donc l’ensemble de la galerie. Cette galerie a 11 côtés et on a besoin d’au moins deux caméras pour la surveiller.
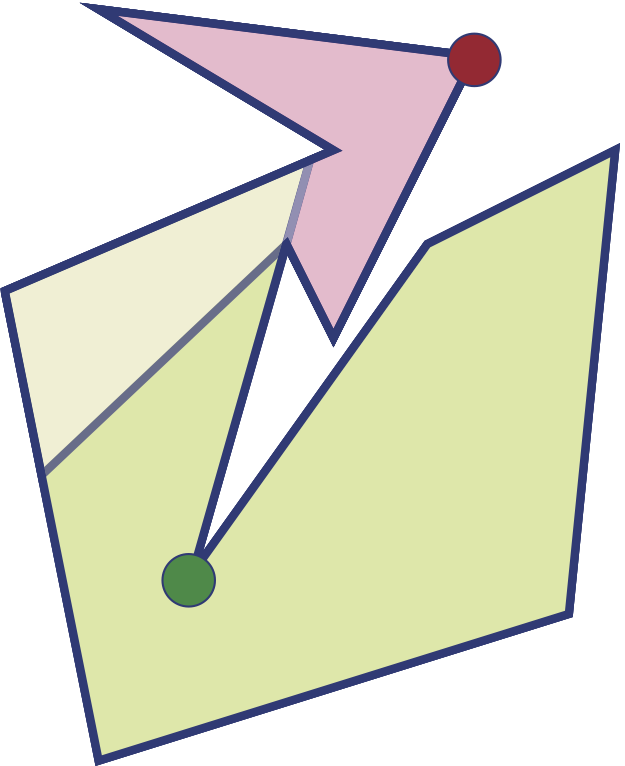Mais, il existe des galeries à 11 côtés pour lesquelles on a besoin de plus de deux caméras. Aussi, dans le problème de la galerie d’art, on se limite à des caméras placées en des sommets du polygone. Le problème de la galerie d’art est le suivant.
Étant donnée une galerie d’art de forme polygonale à n côtés, trouver un nombre \(K(n)\) minimal tel que toute galerie à n côtés peut être surveillée par au maximum \(K(n)\) caméras placées en des sommets du polygone.
Regardons des exemples.
Un galerie d’art en forme de triangle peut être surveillée par une seule caméra placée en n’importe quel sommet. Donc \(K(3) = 1\).
Une galerie d’art en forme de quadrilatère peut être surveillée par une seule caméra. La caméra peut être placée en n’importe quel sommet si le quadrilatère est convexe. Deux positions sont possibles pour la caméra si le quadrilatère est non convexe. Donc \(K(4)=1\).
Toute galerie d’art en forme de polygone convexe peut être surveillée par une seule caméra placée en n’importe quel sommet.
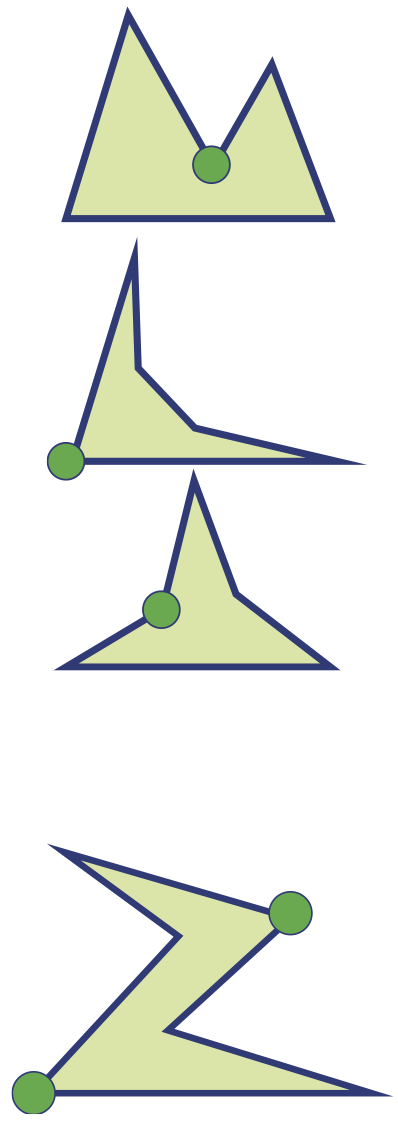En regardant toutes les configurations non convexes possibles, on peut se convaincre que toute galerie d’art en forme de pentagone peut être surveillée par une seule caméra. Donc \(K(5) = 1\).
Par contre, il existe des galeries d’art en forme d’hexagones pour lesquels il faut au moins deux caméras. Donc \(K(6) ≥ 2\). En fait, on montrera que \(K(6) = 2\).
Le problème de la galerie d’art a été posé par Victor Klee en 1973, en réponse à une question de Vasek Chvátal lui demandant un problème intéressant. Vasek Chvátal a donné la solution dès 1975 : il a montré que \(K(n) = n/3\), où \(n/3\) est la partie entière de \(n/3\), soit le plus grand entier inférieur ou égal à \(n/3\).
Mais la question a passionné la communauté de géométrie algorithmique jusqu’à devenir un domaine de recherche étudiant des questions connexes et raffinant les algorithmes pour trouver en pratique des solutions optimales lorsque \(n\) est très grand.
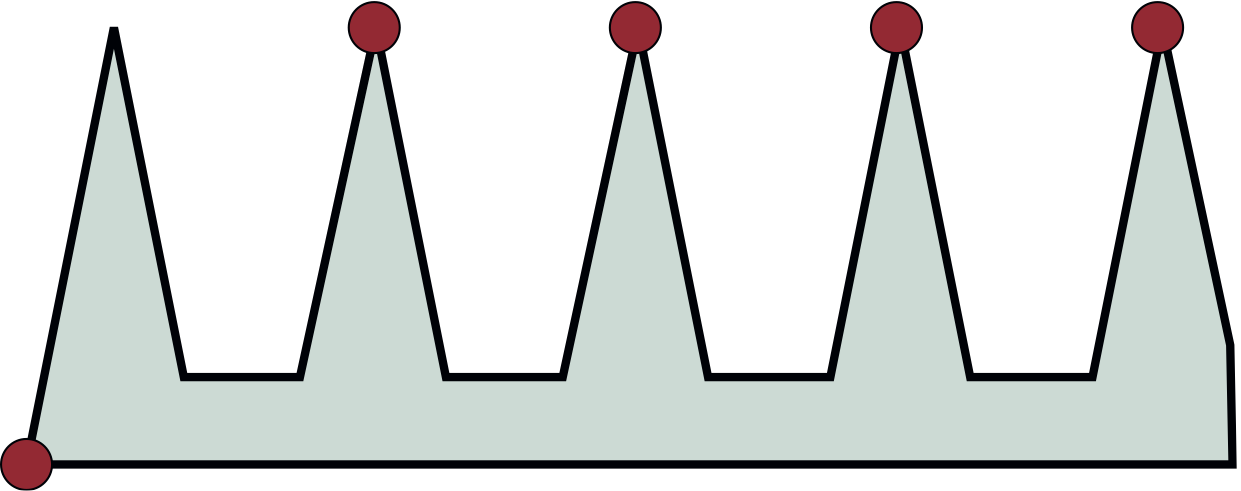
Il est facile de montrer que \(K(n)\geq n/3\). En effet, ce polygone à 15 côtés requiert cinq caméras et on pourrait tronquer le coin extrême droit pour lui donner 16 ou 17 côtés. On peut généraliser cet exemple à un polygone à \(3n, 3n + 1\) ou \(3n + 2\) côtés.
Il reste donc à montrer que \(K(n)\leq n/3\). En 1980, Steve Fisk a simplifié la preuve de Chvátal. Sa preuve est très intéressante et donne un algorithme simple pour placer les caméras. Elle comporte deux étapes :
Première étape : on divise le polygone en triangles, dont tous les sommets sont des sommets du polygone. Voici ce que cela donne pour une galerie à 46 côtés, donc 46 sommets.
Deuxième étape : On colorie les sommets du polygone avec trois couleurs de telle sorte que les sommets de chaque triangle soient de couleur différente.
Dans notre exemple, le rouge apparait 9 fois, le bleu 18 fois et le jaune 19 fois.
Il suffit alors de placer des caméras aux sommets de la couleur apparaissant le moins souvent. Ici, c’est le rouge qui apparait 9 fois. On place les caméras aux 9 sommets rouges.. Dans le cas général, la couleur qui apparait le moins souvent apparait au plus \(\bigl \lfloor n/3 \bigr \rfloor \) fois.
On peut montrer que les deux étapes sont toujours possibles (voir encadré).
Remarques
Une première remarque est que la triangulation n’est pas unique.
Une seconde remarque est que l’algorithme ne donne pas toujours la solution optimale. En effet, cette galerie particulière peut être surveillée avec sept caméras seulement.
En fait, cette galerie, comme la plupart des galeries d’art a une propriété particulière : tous ses angles intérieurs sont de 90° ou de 270°. Un polygone ayant ces propriétés est appelé polygone orthogonal. Pour ces polygones on a une meilleure borne.
Toute galerie en forme de polygone orthogonal à n côtés peut être surveillée par au plus \(\bigl \lfloor n/4 \bigr \rfloor \) caméras.
C’est le théorème de Kahn-Klawe-Kleitman (1980).
La triangulation d’un polygone
Tout polygone à \(n\) côtés peut être décomposé en triangles par l’ajout de diagonales entre des sommets du polygone. La preuve se fait par récurrence sur \(n\), on commence par les polygones à 3 côtés, puis à 4 côtés, puis à 5 côtés, etc. Dans chaque cas, on divise le polygone en deux polygones ayant moins de côtés, donc on se ramène à un cas déjà connu. C’est vrai pour \(n =3\). On suppose maintenant que c’est vrai pour tout polygone à moins de \(n\) côtés. Prenons un polygone à \(n\) côtés et choisissons trois sommets consécutifs. Si le segment joignant les deux sommets extrêmes est contenu à l’intérieur du polygone, alors en divisant ce polygone le long de cette diagonale, on s’est ramené à trianguler deux polygones à 3 et \(n – 1\) côtés.
Sinon, on prend des droites parallèles au segment joignant les deux sommets extrêmes et on rapproche ces droites du sommet médian jusqu’au dernier sommet qu’on attrape.
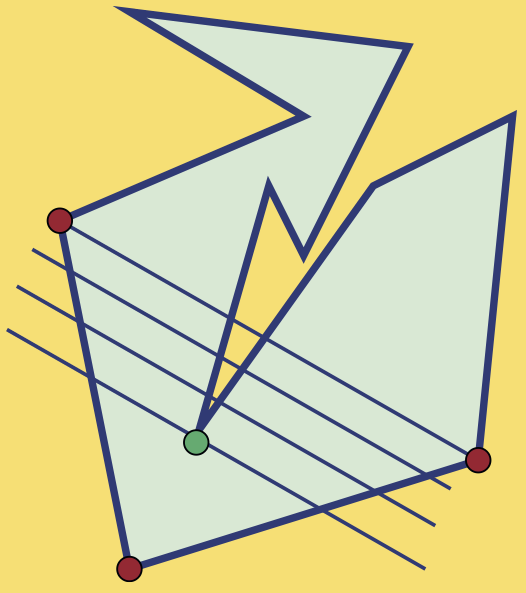
Alors la diagonale entre ce dernier sommet et le sommet médian coupe le polygone en deux polygones à moins de \(n\) côtés qu’on peut trianguler par l’hypothèse d’induction.
Colorier les sommets du polygone de trois couleurs
On commence par colorier les sommets d’un triangle avec les trois couleurs. Pour chaque triangle adjacent, on colorie le dernier sommet avec la couleur non utilisée. Il faut s’assurer qu’on ne rencontre pas d’impossibilité en faisant cela.
L’outil qui permet de s’en assurer est la théorie des graphes. On construit un graphe dont les sommets sont donnés par un point intérieur à chaque triangle.
Quant aux arêtes, on met une arête entre deux sommets du graphe si les deux triangles contenant les sommets partagent un côté.
Ce graphe a une propriété bien particulière : il n’a pas de cycles, c’est-à-dire de suite d’arêtes formant une boucle fermée.
Un graphe avec un cycle
En effet, s’il avait un cycle, alors ce cycle contiendrait un sommet du polygone, entouré de triangles, contredisant le fait que tout sommet du polygone est sur sa frontière. Un graphe sans cycles est appelé un arbre.
On colorie les sommets des triangles de proche en proche en se promenant le long de l’arbre : on choisit un sommet du graphe: il correspond à un triangle dont on colorie les sommets des trois couleurs. On passe à un autre sommet du graphe le long d’une arête. Deux des sommets du triangle correspondant sont déjà coloriés et il reste une seule couleur pour le dernier sommet. On passe à un autre sommet du graphe en suivant une autre arête. Ici encore, le triangle correspondant n’a qu’un sommet non colorié et on le colorie de la dernière couleur. Etc., jusqu’à ce qu’on ait épuisé les sommets du graphe. S’il y avait des cycles on pourrait avoir des impossibilités, selon que l’on arrive d’un côté ou de l’autre du cycle. Mais, sur un arbre, il n’y en a pas.
Ici encore, l’exemple ci-dessous montre qu’on ne peut avoir une meilleure borne.
Les idées de l’algorithme sont les mêmes que celles de l’algorithme de Fisk.
Première étape : on divise le polygone en quadrilatères convexes.
Deuxième étape : on colorie les sommets du polygone avec quatre couleurs de telle sorte que les sommets de chaque quadrilatère soient de couleur différente.
On place ensuite les caméras aux sommets de la couleur apparaissant le moins souvent. Ici ce sont, soit les sommets rouges, soit les sommets jaunes, au nombre de 11. Comme tous les quadrilatères sont convexes et que chacun contient une caméra en un sommet, on surveille bien toute la galerie.
La grande différence avec l’algorithme de Fisk est qu’il n’est pas facile de diviser un polygone orthogonal en quadrilatères convexes. Si on choisit de mauvaises divisions au départ, alors on aboutit à une impossibilité. La preuve que cette division est possible est longue et difficile.
Le problème de la forteresse
Dans ce problème, on veut surveiller tout l’extérieur d’une forteresse de forme polygonale à \(n\) côtés en plaçant des caméras en des sommets du polygone. Soit \(F(n)\) la borne minimale sur le nombre de caméras pour toute forteresse à \(n\) côtés. O’Rourke et Wood ont montré en 1983 que \(F(n)=\bigl \lfloor(n+1)/2\bigr \rfloor =\bigl \lceil n/2\bigr \rceil\) où \(\bigl \lceil n/2\bigr \rceil\) est le plus petit entier supérieur ou égal à \(n/2\).
En prenant un polygone régulier à n côtés, ou encore un polygone convexe, on voit que \(F(n) \geq \bigl \lceil n/2\bigr \rceil\).
Pour montrer l’autre inégalité, soit \(F(n) \leq \bigl \lceil n/2\bigr \rceil\), on va utiliser des triangulations comme dans la preuve de Fisk, mais la preuve est plus complexe. Prenons une forteresse.
Comme elle n’est pas convexe, on va prendre le plus petit convexe la contenant, appelé son enveloppe convexe, dont on va trianguler la partie à l’extérieur du polygone.
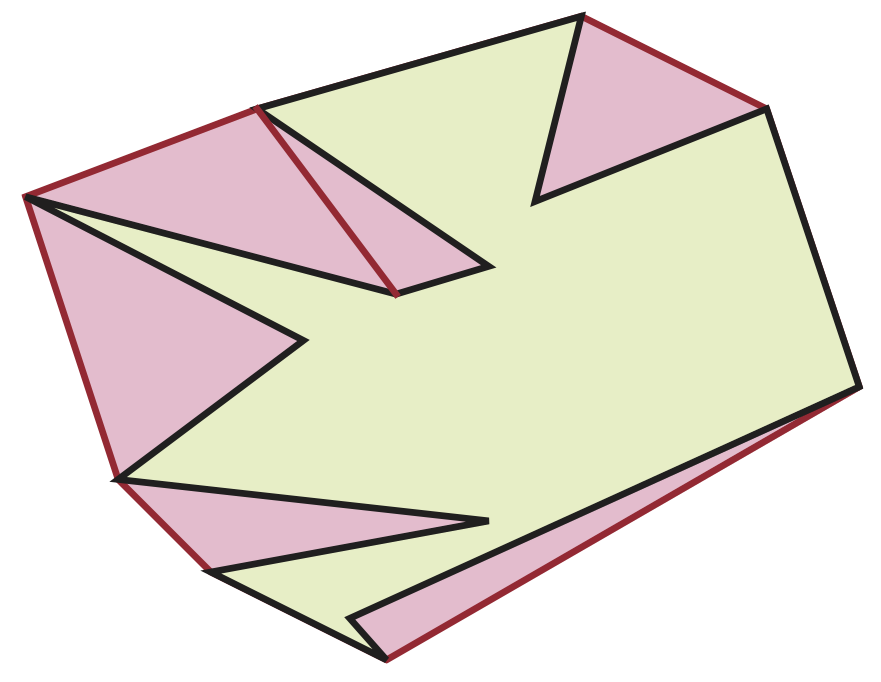
Remarquons qu’on a deux types de sommets : des sommets qui sont à l’intérieur de l’enveloppe convexe, qu’on appelle sommets intérieurs et des sommets qui sont sur la frontière de l’enveloppe convexe qu’on appelle sommets extérieurs.
On sépare un sommet extérieur en deux sommets distincts proches l’un de l’autre. De cette manière on a ouvert le polygone qui est devenue une ligne brisée entre \(n+1\) points. Ces \(n+1\) points sont les sommets d’un nouveau graphe, dont les arêtes sont les segments de droite du polygone ouvert et ceux ajoutés dans la triangulation.
On va rajouter un \((n+2)^{\text{ième}}\) sommet à l’extérieur du polygone, que l’on appelle sommet auxiliaire et que l’on ajoute aux autres sommets du graphe. On joint le sommet auxiliaire à tous les sommets extérieurs par des courbes qui ne s’intersectent pas. Ces courbes sont de nouvelles arêtes du graphe. En pratique, on aura deux arêtes joignant le sommet auxiliaire aux deux sommets dédoublés, une de chaque côté de l’enveloppe convexe.
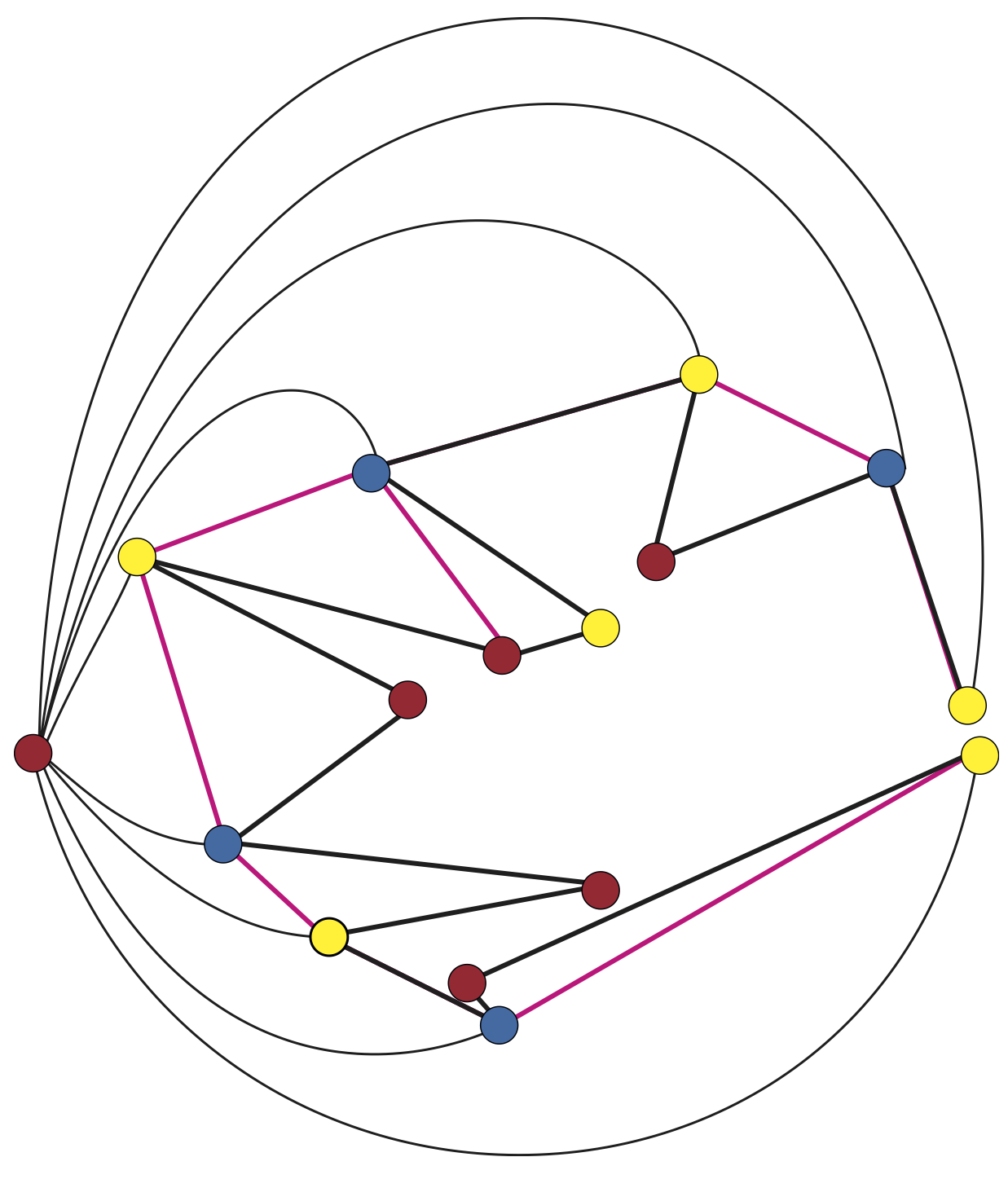
Regardons ce graphe. Il découpe sur le plan des régions fermées et bornées limitées chacune par trois arêtes, que l’on appellera des « faces ». Ces « faces » sont des triangles si les arêtes sont des segments de droite et des triangles généralisés si certaines arêtes sont des courbes. On va colorier tous les sommets avec trois couleurs de telle sorte que les sommets de chaque face soient de couleur différente. C’est toujours possible : on peut faire le même argument que dans l’encadré sur le coloriage des sommets du polygone de trois couleurs (plus de détails dans l’encadré).
On prend les sommets de la couleur qui apparait le moins souvent et on place des caméras en ces points.
Premier cas
Si cette couleur n’est pas celle du sommet auxiliaire, on a une solution avec \(\bigl \lfloor(n + 2)/3 \bigr \rfloor \leq \bigl \lceil n/2\bigr \rceil\) caméras. Ces caméras permettent de surveiller l’extérieur de la forteresse (voir encadré). C’est le cas pour notre exemple et les quatre caméras aux sommets bleus permettent de surveiller l’extérieur de la forteresse.
Deuxième cas
Si la couleur qui apparaît le moins souvent est celle du sommet auxiliaire, on met les caméras aux sommets de la deuxième couleur qui apparait le moins souvent. Cette couleur apparaît au plus \(\bigl \lfloor(n + 1)/2 \bigr \rfloor = \bigl \lceil n/2\bigr \rceil\) fois (voir la page problèmes pour l’égalité). Il est à remarquer qu’on est toujours dans ce deuxième cas quand la forteresse est un polygone convexe. Quant au sommet dédoublé, on place une caméra en ce sommet dès qu’au moins un des deux sommets est de la couleur choisie.
Conclusion
Les preuves des théorèmes sur la galerie d’art et la forteresse utilisent la triangulation des polygones et des arguments de théorie des graphes. Ces deux outils sont très polyvalents et ont de multiples applications. C’est une des raisons de la puissance des mathématiques dans la résolution de problèmes. Un même outil construit pour un problème donné peut avoir des applications très loin du problème pour lequel il a été construit.
Pourquoi l’algorithme de la forteresse fonctionne
Avant de lire cette partie, essayez d’exécuter l’algorithme sur des exemples tel que proposé dans la page problèmes. Il y a deux choses à vérifier : i) que pour chaque face, on peut colorier ses sommets de couleurs différentes, et ii) que les caméras surveillent tout l’extérieur de la forteresse.
i) Pour chaque face, on peut colorier ses sommets de couleurs différentes.
Construisons un graphe « dual » dont les sommets (les étoiles vertes sur la figure) sont donnés par un point dans chaque face, et mettons une arête (en trait pointillé épais) entre deux sommets quand deux faces partagent un côté. Ce graphe dual est un arbre : il n’a pas de cycle.
En effet, l’objet géométrique formé par la réunion des faces est un objet d’un seul morceau, sans trou. C’est pour cela qu’on a séparé un sommet en deux sommets, sinon on aurait un trou. Remarquons que les \(n+2\) sommets sont tous sur la frontière de l’objet géométrique. S’il y avait un cycle dans le graphe dual, les faces correspondant aux sommets du cycle entoureraient un des sommets. Contradiction !
ii) Les caméras surveillent tout l’extérieur de la forteresse.
L’extérieur de la forteresse comprend deux parties : l’extérieur de l’enveloppe convexe et l’extérieur de la forteresse qui est situé à l’intérieur de l’enveloppe convexe. Il est facile de montrer que les caméras surveillent cette deuxième partie. En effet, celle-ci est divisée en triangles et on a une caméra dans chaque triangle.
Montrons maintenant que les caméras surveillent l’extérieur de l’enveloppe convexe.
Remarquons que la couleur choisie pour placer les caméras à des sommets est toujours une couleur différente de celle du sommet auxiliaire. Supposons que le sommet auxiliaire est coloré en rouge. Comme tous les côtés de l’enveloppe convexe sont des côtés d’une face à laquelle appartient le sommet auxiliaire, alors les deux autres sommets de chaque face doivent être bleu et jaune. Donc, les sommets de l’enveloppe convexe (qui sont les sommets extérieurs) alternent entre le bleu et le jaune. Par suite, les caméras sont placées à un sommet sur deux de l’enveloppe convexe (et on a deux caméras adjacentes dès qu’on a un nombre impair de sommets extérieurs). On a déjà vu qu’en plaçant une caméra tous les deux sommets on surveille l’extérieur d’un polygone convexe. Donc, les caméras surveillent l’extérieur de l’enveloppe convexe.
