Zia pense que son GPS est défectueux, ce que nie le vendeur. Souhaitant valider sa position d’une autre manière, elle a fait une recherche pour savoir comment les capitaines procédaient avant le GPS.

Zia
Je pense que mon GPS est défectueux et j’ai fait une recherche pour savoir comment déterminer ma position en longeant une côte sans cet instrument.

Léo
Et comment vas-tu faire ?

Zia
Tu sais comment on exprime la mesure d’un angle au centre d’un cercle ainsi que l’arc qu’il intercepte ?

Léo
Oui. En radians, c’est la longueur de l’arc mesurée en sens antihoraire divisée par le rayon du cercle. Pour avoir la mesure en degrés, on multiplie par \(180/\pi\). L’angle au centre et l’arc qu’il intercepte sont des éléments différents, mais leur mesure est la même.

Zia
Tu sais aussi ce qu’est un angle inscrit ?

Léo
Bien oui, c’est un angle dont le sommet est sur la circonférence du cercle.

Zia
Sais-tu montrer que la mesure d’un angle inscrit est égale à la moitié de la mesure de l’angle au centre interceptant le même arc ?

Léo
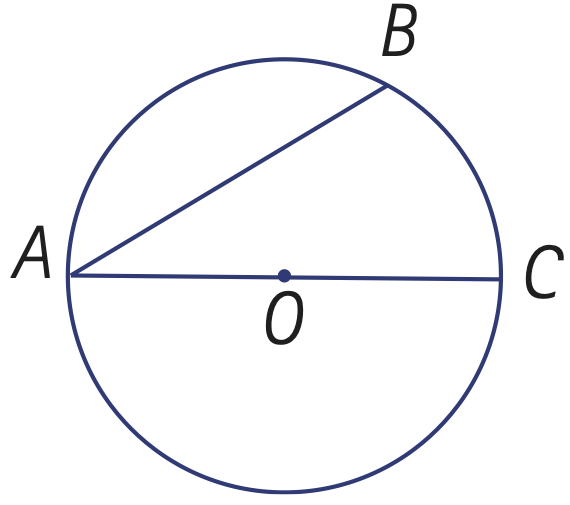
Bien sûr. Supposons que le centre du cercle est sur un des côtés de l’angle. Je joins le centre O du cercle à l’extrémité B du côté AB. J’ai alors deux angles, BAC et BOC qui interceptent le même arc, l’un est un angle au centre et l’autre un angle inscrit. Je peux alors les comparer, voici comment.

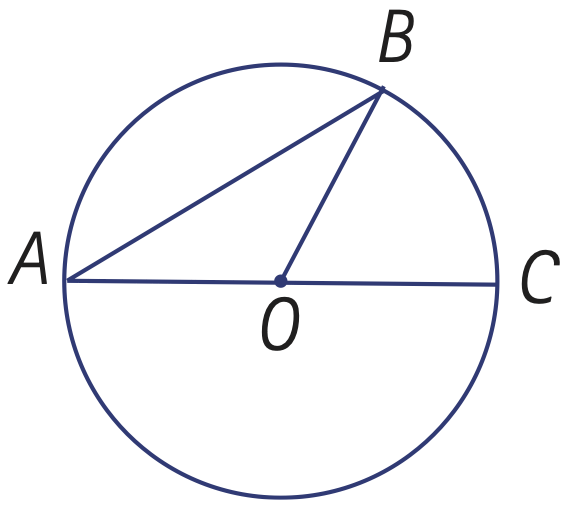Le triangle AOB est un triangle isocèle; les angles opposés aux côtés congruents sont eux aussi congruents.

Par conséquent les angles BAO et ABO sont de même mesure, que je note par \(\alpha\). Comme la somme des angles d’un triangle est 180°, l’angle AOB est \(180° – 2\alpha\). De plus, l’angle AOC est un angle plat, on a donc
\[\begin{array}{r c l}\angle COB &=&180° – \angle AOB \\ &= &180 – (180° – 2\alpha) = 2\alpha.\end{array}\]

Lorsqu’un des côtés passe par le centre du cercle, la mesure de l’angle inscrit est donc égale à la moitié de la mesure de l’arc intercepté, qui est celle de l’angle au centre.

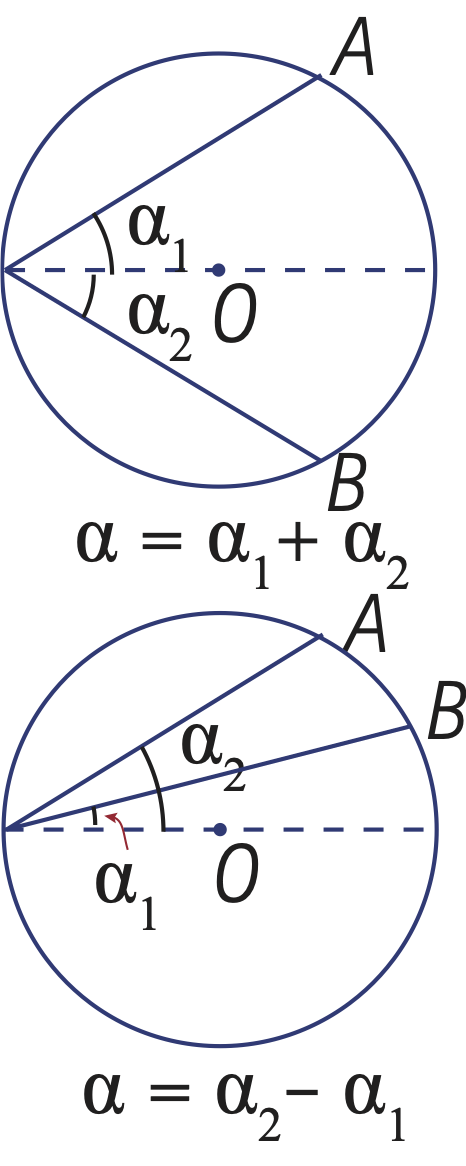
C’est vrai aussi lorsque le centre du cercle est compris à l’intérieur ou à l’extérieur de l’angle, il suffit de faire une somme ou une différence d’angles.

Zia
Alors tu es « capable » de comprendre c’est quoi un arc capable. Tu prends une corde AB dans un  cercle: elle le divise en deux arcs et sur chacun de ces arcs, tous les points déterminent forcément avec A et B des angles ayant une valeur constante. On dit de chaque arc qu’il est le lieu géométrique des points d’où « on peut voir » le segment AB sous un même angle. Les deux angles \(\alpha\) et \(\beta\) sont supplémentaires et on appelle chacun des arcs de cercle un arc capable¹.

Léo
Et ça permet de connaître la position d’un navire en mer ?

Zia
Attends ! Je t’explique. Supposons que le capitaine d’un navire, désirant déterminer sa position, mesure l’angle entre sa position et deux points : un phare, un clocher d’église ou n’importe quels autres points identifiés sur sa carte.

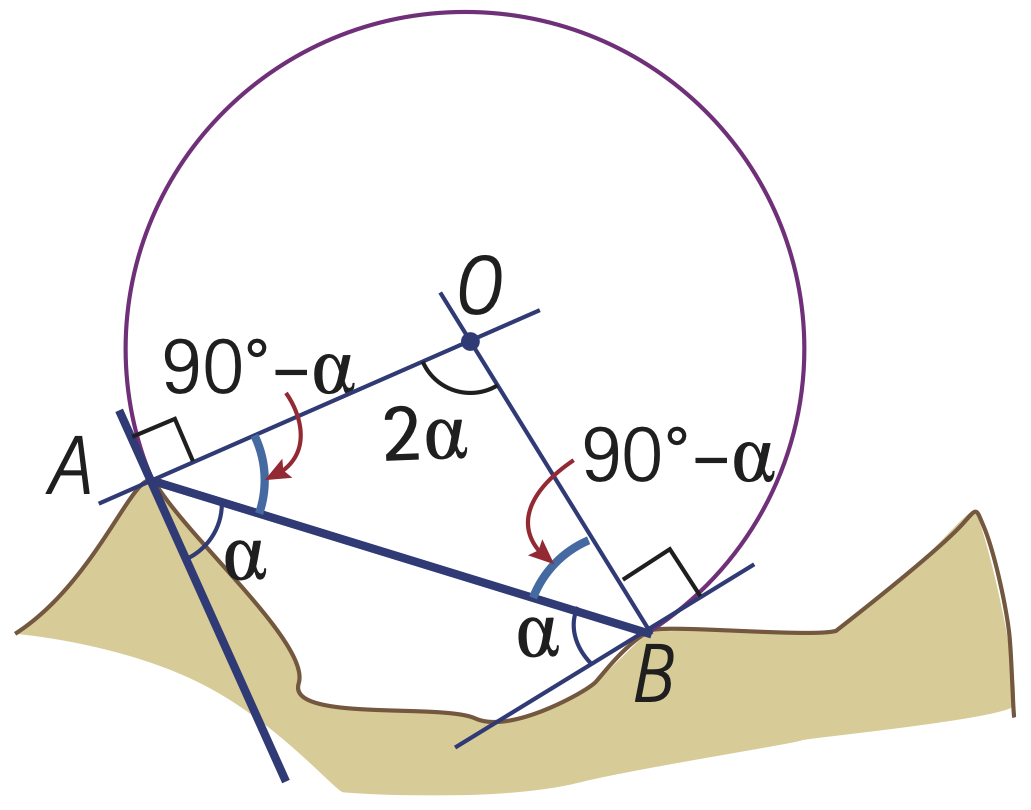
Supposons qu’il obtient une mesure d’angle \(\alpha\). Cet angle est le même partout sur l’arc capable relatif à l’angle α et aux points A et B. On peut alors montrer qu’aux points A et B, un des côtés de l’angle se superpose au segment AB et le second côté à la tangente au cercle². C’est pourquoi le capitaine trace, du côté de la terre, un segment de droite qui forme un angle de sommet A et de mesure α avec le segment AB.

Il trace ensuite la perpendiculaire à cette droite par le point A. Le centre du cercle est sur ce segment de droite, puisque le rayon est perpendiculaire à la tangente.

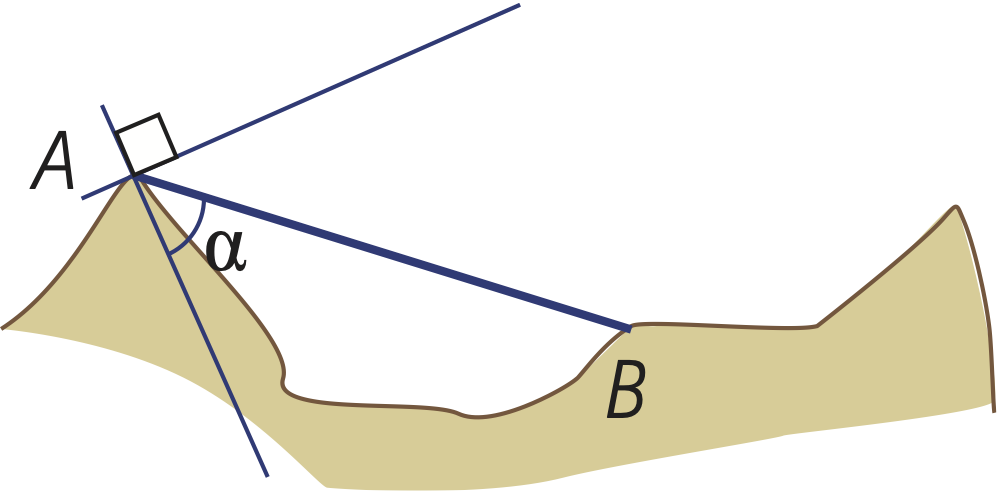
Il fait la même chose en formant un angle de mesure \(\alpha\) dont le sommet est B.

Les deux perpendiculaires se rencontrent en un point O, qui est le centre du cercle cherché. Elles forment alors un triangle dont deux angles sont de \(90° – \alpha\), de sorte que l’angle au centre est de
\[180° – 2(90° – \alpha) = 2\alpha.\]

Léo
Le capitaine peut alors savoir qu’il est quelque part sur cet arc capable, mais il ne connaît pas sa position exacte.

Zia
Tu as raison ! C’est pourquoi il prend le relevé d’un troisième point C, trace le segment BC sur sa carte, et prend la mesure \(\beta\) de l’angle entre sa position et le segment BC. Il refait ensuite la même construction pour trouver le centre O’ du cercle pour lequel l’angle BO’C mesure \(2\beta.\) Puis il trace un second arc capable.

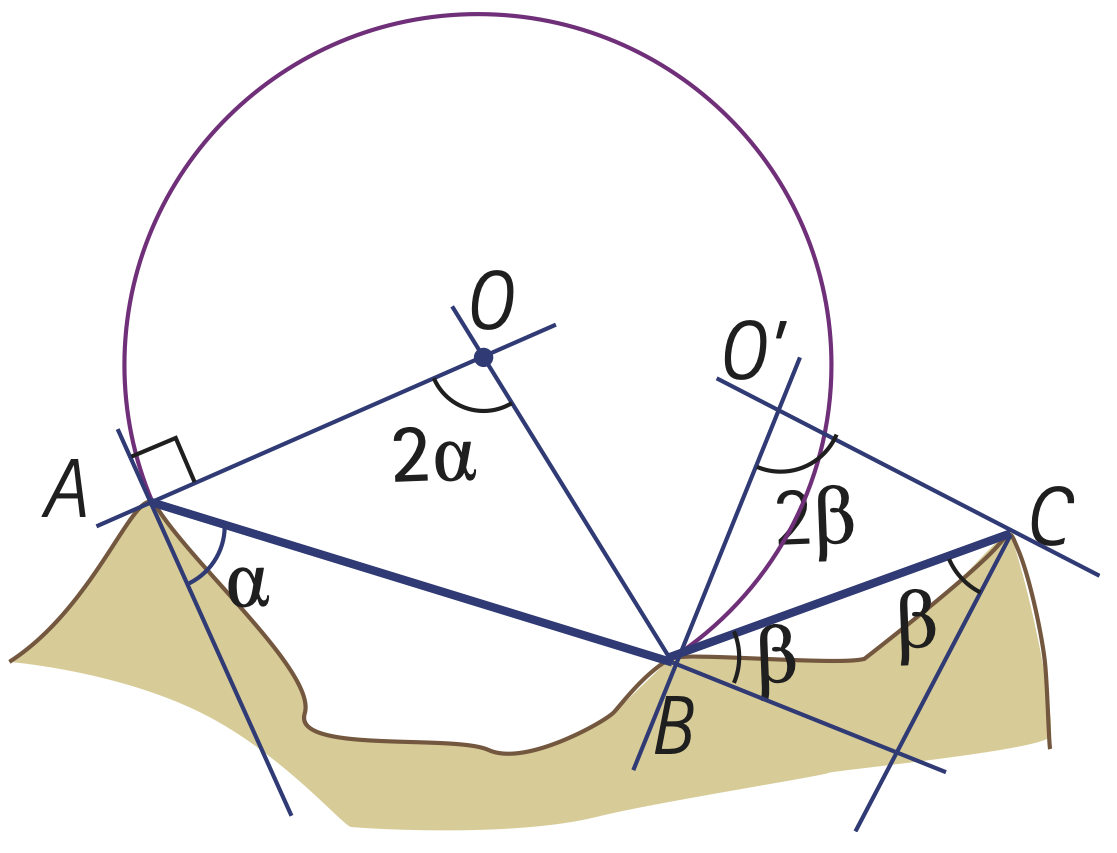
Tadam ! Le navire se situe à l’intersection de ces deux arcs capables.

Léo
C’est super ! Et tu vas essayer ça à ta prochaine sortie en voilier ?

Zia
Oui, je vais mesurer deux angles et noter la position que me donne le GPS. Je pourrai alors vérifier si mon GPS est fiable. S’il donne des valeurs erronées, j’aurai des preuves pour justifier ma réclamation. Le vendeur ne pourra plus nier.

Sextant, crédit : U.S. Geological Survey

Avant 1730, on se servait surtout de l’arbalestrille pour mesurer des angles. À partir
de 1731, il sera remplacé par l’octant puis par le sextant, inventé, indépendammant par John Hadley 1682-1744), un mathématicien et astronome britannique, et Thomas Godfrey (1704-1749), un inventeur américain.

PDF